
Tilastot ovat järjestely tilastolliset testit, joita analyytikot käyttävät tehdä päätellen annetut tiedot. Näiden testien avulla voimme tehdä päätöksiä tietojen perusteella. On olemassa laaja valikoima tilastollisia testejä. Tilastollisen testin valinta perustuu tietojen rakenteeseen, tietojen jakamiseen ja muuttuvaan tyyppiin.,Tilastoissa on monia erityyppisiä testejä,kuten t-testi,Z-testi, khiin neliötesti ,anova-testi, binomitesti, yksi näytteen mediaanitesti jne.
tilastollisen testin valitseminen-
parametrisia testejä käytetään, jos tiedot ovat normaalisti jakautuneet .Parametrinen tilastollinen testi tekee oletuksen siitä, väestön parametrit ja jakaumat, että tiedot tuli. Tällaisia testejä ovat muun muassa t-testit,z-testit ja anova-testit, joiden oletetaan olevan peräisin normaalijakaumasta.,
Z-testi z-testi on tilastollinen testi, jota käytetään määrittämään, onko kahden populaation keskiarvojen ovat erilaisia, kun varianssit ovat tunnettuja ja otoskoko on suuri. Z-testissä väestön keskiarvoa verrataan.Käytetyt parametrit ovat populaation keskiarvo ja populaation keskihajonta. Z-testillä validoidaan hypoteesi, jonka mukaan vedetty näyte kuuluu samaan populaatioon.,
Ho: Näytteen keskiarvo on sama kuin populaation keskiarvo(nollahypoteesi)
Ha: Näytteen keskiarvo ei ole sama kuin populaation keskiarvo(Vaihtoehtoinen hypoteesi)
z = (x — µ) / (σ / √n),
jossa x=näytteen keskiarvo, u=populaation keskiarvo, σ / √n = perusjoukon keskihajonta.
Jos z-arvo on pienempi kuin kriittinen arvo hyväksy nollahypoteesi muu hylkää nollahypoteesin.
T-testi-t-testi keskiarvo kahden antanut näytteitä verrataan. T-testiä käytetään, kun populaatioparametreja (keskiarvo ja keskihajonta) ei tunneta.,
parittaiset T-testi-testit kahden muuttujan erolle samasta populaatiosta( ennen ja jälkeen testin pisteet). Esimerkiksi – harjoittelijan harjoitusohjelman suoritusarvio ennen ohjelman päättymistä ja sen jälkeen.
Riippumaton T-testi – riippumattomien t-testi, jota kutsutaan myös kahden otoksen t-testi tai studentin t-testi on tilastollinen testi, joka määrittää, onko tilastollisesti merkitsevä ero tarkoittaa kaksi erillistä ryhmää.Esimerkiksi-vertaamalla poikia ja tyttöjä väestössä.,
yksi näyte t-testi – yksittäisen ryhmän keskiarvoa verrataan annettuun keskiarvoon. Esimerkiksi-tarkistaa myynnin kasvu ja lasku, jos keskimääräinen myynti annetaan.
t = (x1 — x2) / (σ / √n1 + σ / √n2),
missä x1 ja x2 ovat keskiarvo näyte 1 ja näyte 2 vastaavasti.
ANOVA Test – Analysis of variance (ANOVA) on tilastollinen tekniikka, jolla tarkistetaan, ovatko kahden tai useamman ryhmän keinot merkittävästi erilaisia keskenään. ANOVA tarkistaa yhden tai useamman tekijän vaikutuksen vertaamalla eri näytteiden keinoja., Jos käytämme t-testin sijaan ANOVA-testi se ei ole luotettava, koska näytteitä on enemmän kuin kaksi ja se antaa virheen seurauksena.
hypoteesi on testattu ANOVA on
Ho: Kaikki parit näytteet ovat samat eli, kaikki näyte tarkoittaa, ovat tasa-arvoisia
Ha: vähintään yhdet näytteet on merkittävästi erilainen
anova-testi, me laskea F-arvo ja verrata sitä kriittistä arvoa
F:= ((SSE1 — SSE2)/m)/ SSE2/n-k, jossa
SSE = jäljellä oleva summa neliöt
m = useita rajoituksia
k = määrä riippumattomia muuttujia
Ei parametrinen tilastollinen testi – Kuin parametriset testit käytetään, kun tietoja ei ole normaalisti jakautunut. Ei-parametrisiin testeihin kuuluu chi-neliötesti.
Chi-square test( χ2 test)- chi-square test käytetään vertailemaan kahta kategorista muuttujaa., Laskeminen Chi-Neliö tilastotieto arvo ja vertaamalla sitä vastaan kriittinen arvo Chi-Neliö jakelun avulla voidaan arvioida, onko havaittu taajuus ovat merkittävästi erilaisia kuin odotettu taajuus.
hypoteesi testataan khiin neliö-on-
Ho: Muuttuja x ja Muuttujan y ovat riippumattomia
Ha: Muuttuja x ja Muuttujan y eivät ole riippumattomia.,
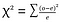
where o=observed , e=expected.
Leave a Reply