
Statistik er arrangementet af statistiske tests, som analytikere bruge til at gøre slutning ud fra de givne data. Disse tests gør det muligt for os at træffe beslutninger på baggrund af observeret mønster fra data. Der er en bred vifte af statistiske tests. Valget af hvilken statistisk test til at udnytte afhænger af strukturen af data, fordelingen af data, og variabel type.,Der er mange forskellige typer af tests i statistik som t-test,test-test,chi-s .uare test, anova test ,binomial test, en prøve median test osv.
valg af statistisk test-
parametriske test anvendes, hvis dataene normalt distribueres .En parametrisk statistisk test gør en antagelse om populationsparametrene og de distributioner, som dataene kom fra. Disse typer af test omfatter t-test, z-test og anova test, som antager data er fra normal fordeling.,
test-test – en test-test er en statistisk test, der bruges til at bestemme, om to populationsmidler er forskellige, når afvigelserne er kendt, og prøvestørrelsen er stor. I test-test middelværdi af befolkningen sammenlignes.De anvendte parametre er populationsmiddelværdi og populationsstandardafvigelse. Z-test bruges til at validere en hypotese om, at den udtrukne prøve tilhører den samme population.,
Ho: Stikprøve middelværdien er den samme som populationsmiddelværdien(nulhypotesen)
Ha: Prøven betyder er ikke samme som at populationsmiddelværdien(Alternative hypotese)
z = (x — μ) / (σ / √n),
hvor: x=prøven betyder, u=populationsmiddelværdi, σ / √n = populationens standardafvigelse.
Hvis value-værdien er mindre end kritisk værdi, accepter nulhypotesen ellers Afvis nulhypotesen.
T-test-i t-test sammenlignes gennemsnittet af de to givne prøver. En t-test anvendes, når populationsparametrene (middel-og standardafvigelse) ikke er kendt.,
Parret T-Test-Test for forskellen mellem to variabler fra samme population( præ – og post test-score). For eksempel-i et træningsprogram præstation score af praktikanten før og efter afslutningen af programmet.
Uafhængig T-test – Den uafhængige t-test, som også kaldes de to sample t-test eller student ‘ s t-test, er en statistisk test, der afgør, om der er en statistisk signifikant forskel mellem de midler, der i to uafhængige grupper.For eksempel-sammenligning af drenge og piger i en befolkning.,
en prøve t-test – gennemsnittet af en enkelt gruppe sammenlignes med et givet middel. For eksempel-for at kontrollere stigningen og faldet i salget, hvis det gennemsnitlige salg er givet.
t = (11 -22) / (n1 / n1 n1+./n n2),
hvor11 og22 er gennemsnittet af henholdsvis prøve 1 og prøve 2.
ANOVA Test – variansanalyse (ANOVA) er en statistisk teknik, der bruges til at kontrollere, om midlerne til to eller flere grupper er signifikant forskellige fra hinanden. ANOVA kontrollerer virkningen af en eller flere faktorer ved at sammenligne midlerne til forskellige prøver., Hvis vi bruger en t-test i stedet for ANOVA-test, vil den ikke være pålidelig, da antallet af prøver er mere end to, og det vil give fejl i resultatet.
hypotesen, der testes i ANOVA, er
Ho: alle par prøver er ens, dvs., alle prøven hjælp er lige
Ha: mindst et par af prøver, der er væsentlig forskellig
I anova test vi beregne F-værdi og sammenligne det med den kritiske værdi
F= ((SSE1 — SSE2)/m)/ SSE2/n-k, hvor
SSE = residual sum af kvadrater
m = antallet af begrænsninger
k = antallet af uafhængige variable
Ikke-parametriske statistiske test – Ikke-parametriske tests anvendes, når data ikke er normalfordelte. Ikke parametriske tests omfatter chi-s .uare test.
Chi-s .uare test (22 test)- chi-s .uare test bruges til at sammenligne to kategoriske variabler., Beregning af Chi-Square statistik værdi og sammenligne det mod en kritisk værdi fra Chi-Square distribution giver mulighed for at vurdere, om den observerede frekvens, der er væsentlig forskellig fra den forventede hyppighed.
den hypotese, der testes for chi-kvadrat, er-
Ho: variabel and og variabel y er uafhængige
Ha: variabel and og variabel y er ikke uafhængige.,
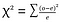
where o=observed , e=expected.
Leave a Reply